مكابح الضغط

حساب الزاوية – كيفية حساب زاوية الثني للمنحنيات ذات القوس الكبير

حساب الزاوية – كم عدد الانحناءات المطلوبة للقوس الكبير وكيفية حساب زاوية الانحناء

الطريقة ١

كيفية ثني قوس؟ (بدون قالب مخصص)

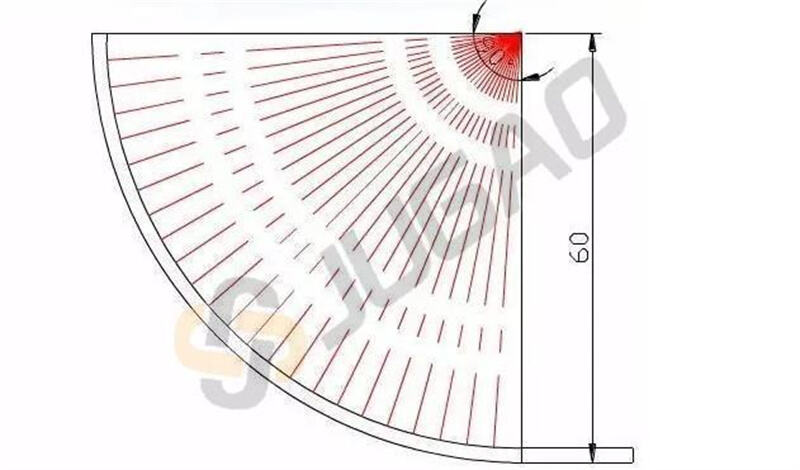
كما هو موضح أعلاه:

سمك الصفيحة T = ٢ مم، الزاوية المركزية = ٩٠°

١. احسب طول القوس:

طول القوس L = ٩٠° × π ÷ ١٨٠° × نصف قطر المحور المحايد R59 = ٩٢,٦٣ مم

٢. اختر أدوات الثني:

استخدم شفرة مستقيمة للقالب العلوي وقالبًا سفليًا بزاوية 8V (عند ثني قوس، اختر أقل عرض مسموح به لفتحة الـ V، وعادةً ما يكون هذا العرض بين 4T و6T).

3. احسب التغذية لكل ثنية:

التغذية لكل ثنية = نصف عرض فتحة الـ V المختارة في القالب السفلي.

4. احسب عدد الثنيات المطلوبة:

عدد الثنيات = طول القوس L (92.63 مم) ÷ (عرض فتحة الـ V ÷ 2 = 4 مم) ≈ 23 ثنية.

5. احسب بعد التموضع لكل ثنية:

بعد حساب بعد التموضع للثنيّة الأولى، قلل البعد في كل ثنية لاحقة بمقدار 4 مم (يجب تخطيط تسلسل الثني من الداخل إلى الخارج).

6. وأخيرًا، احسب زاوية الثنية لكل ثنية:

ويستند ذلك إلى الصيغ المثلثية القياسية.

7. اختبار الثني:

بعد التحقق من الحسابات، قم بإجراء ثنيات تجريبية على مواد خردة للتأكد من الزاوية قبل المتابعة مع القطعة الفعلية.

الطريقة ٢

خذ الرسم البياني التالي في الاعتبار:

سماكة الصفيحة: ٢ مم

زاوية الثني: ١٢٠°

نصف قطر ثني السطح الخارجي: ٣٠ مم

نصف قطر المحور المحايد: ٢٩ مم

في حالة الثني القوسي، يُحسب الطول المطور استنادًا إلى طول قوس المحور المحايد. ولذلك، يجب أيضًا حساب عدد الثنيات وزاوية كل ثنية باستخدام طول قوس المحور المحايد.

يقع المحور المحايد على مسافة تساوي نصف سماكة الصفيحة من السطح الداخلي.

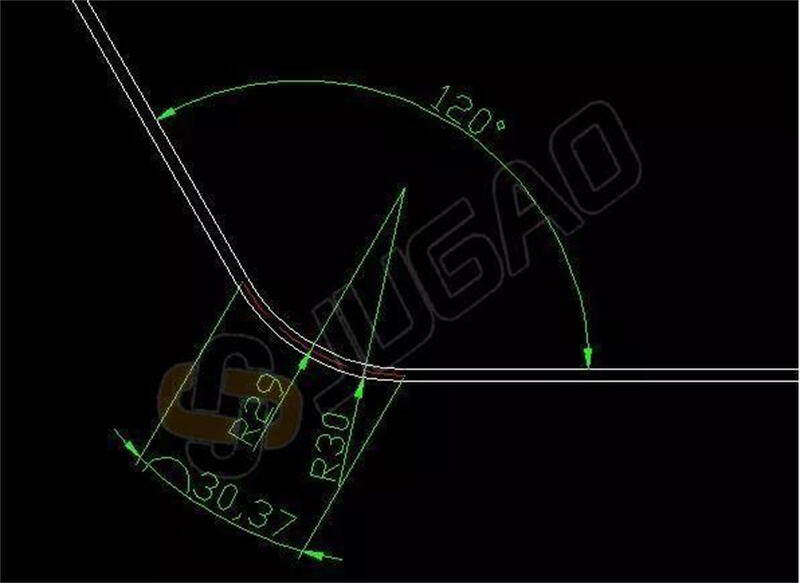
بالنسبة الثني القوسي الموضح أعلاه، كم عدد الثنيات المطلوبة وما هي زاوية الثني لكل منها؟

إذا كانت التغذية لكل انحناء تساوي ٢ مم:

• عدد الانحناءات = طول القوس ÷ ٢ مم = ٣٠٫٣٧ ÷ ٢ ≈ ١٥ انحناءً

• زاوية الانحناء لكل انحناء

= ١٨٠ − { (٢ ÷ طول القوس) × (١٨٠ − مجموع زوايا الانحناء) }

= ١٨٠ − { (٢ ÷ ٣٠٫٣٧) × ٦٠ }

= ١٧٦°

إذا لم يمكن قياس طول القوس مباشرةً أثناء التشغيل، فيمكن أيضًا حساب زاوية الانحناء باستخدام الصيغة التالية:

زاوية الانحناء لكل انحناء = ١٨٠ − { (٢ ÷ (π × نصف قطر المحور المحايد)) × ١٨٠ }

= ١٨٠ − { (٢ ÷ (٣٫١٤ × ٢٩)) × ١٨٠ }

= ١٧٦°

للاستخدام بتغذية مختلفة لكل انحناء (مثل: ٣ مم)، يُكفي استبدال القيمة «٢» في الصيغ أعلاه بالقيمة المطلوبة للتغذية.

توفر هذه الصيغ قيمًا نظرية. وفي الواقع، ينبغي إجراء تعديلات بناءً على نتائج الاختبارات، مستخدمًا القيم المحسوبة كنقطة انطلاق.