เครื่องดัดเบรค

ค่า K คือค่าคงที่อิสระที่ใช้อธิบายลักษณะการพับหรือคลี่ของแผ่นโลหะภายใต้พารามิเตอร์ทางเรขาคณิตต่างๆ หลากหลายรูปแบบ นอกจากนี้ยังเป็นค่าอิสระที่ใช้ในการคำนวณค่าชดเชยการพับ (BA) ภายใต้เงื่อนไขหลายประการ เช่น ความหนาของวัสดุ รัศมีการพับ/มุมพับ เป็นต้น รูปที่ 4 และ 5 แสดงรายละเอียดเพิ่มเติมเกี่ยวกับนิยามอย่างละเอียดของค่า K

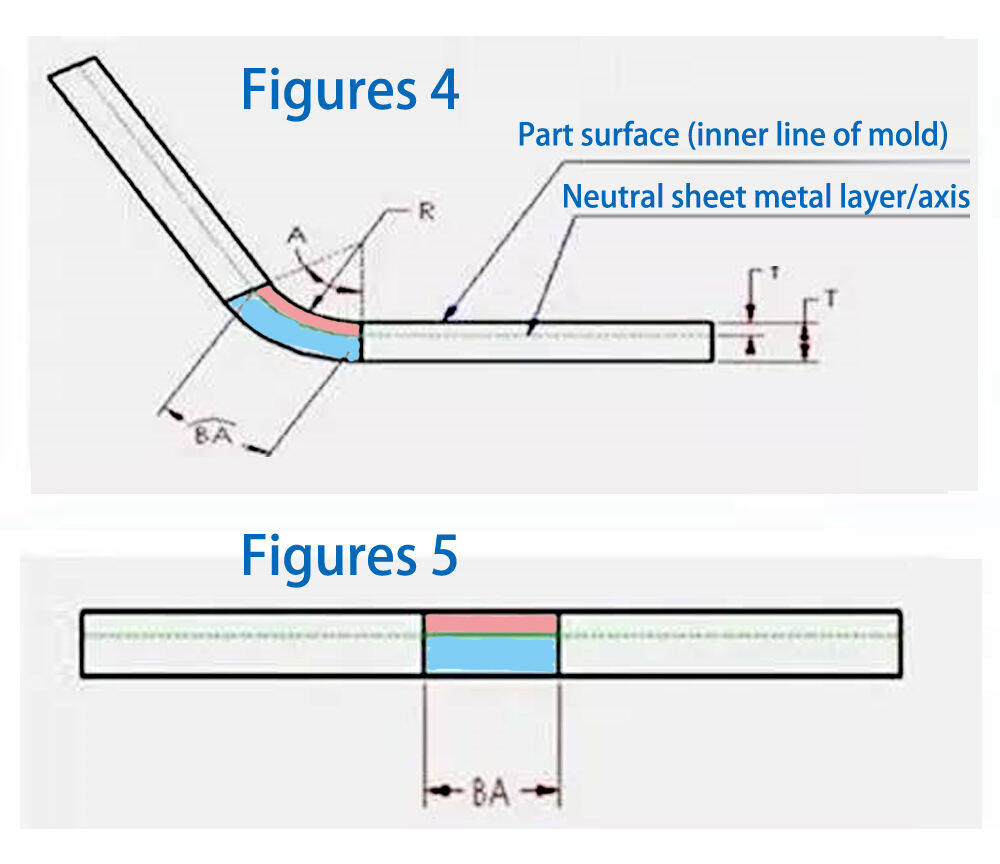
ภายในความหนาของชิ้นส่วนโลหะแผ่น จะมีชั้นกลางหรือแกนที่เป็นกลางอยู่ชั้นหนึ่ง ซึ่งชั้นที่เป็นกลางนี้ตั้งอยู่ในเขตการดัดโค้ง และจะไม่ยืดหรือหดตัว นี่คือบริเวณเดียวของโลหะแผ่นที่ไม่เกิดการเปลี่ยนรูปในระหว่างกระบวนการดัดโค้ง ซึ่งแสดงไว้ในรูปที่ 4 และ 5 เป็นเส้นแบ่งระหว่างพื้นที่สีชมพูและสีน้ำเงิน ในระหว่างกระบวนการดัดโค้ง พื้นที่สีชมพูจะถูกบีบอัด ขณะที่พื้นที่สีน้ำเงินจะยืดออก หากชั้นที่เป็นกลางไม่เกิดการเปลี่ยนรูป ความยาวของส่วนโค้งในชั้นที่เป็นกลางภายในเขตการดัดโค้งจะเท่ากันทั้งในสถานะที่ถูกดัดโค้งและในสถานะที่คลี่เรียบ ดังนั้น BA (การชดเชยการดัด) ควรจะเท่ากับความยาวของส่วนโค้งในชั้นที่เป็นกลางภายในเขตการดัดโค้งของชิ้นส่วนโลหะแผ่น ซึ่งส่วนโค้งนี้แสดงเป็นสีเขียวในรูปที่ 4 ตำแหน่งของชั้นที่เป็นกลางขึ้นอยู่กับคุณสมบัติเฉพาะของวัสดุ เช่น ความเหนียว สมมติว่าชั้นที่เป็นกลางตั้งอยู่ที่ระยะ "t" จากผิว โดยวัดความลึก t จากผิวของชิ้นส่วนโลหะแผ่นเข้าไปในทิศทางความหนาของชิ้นงาน ดังนั้น รัศมีของส่วนโค้งชั้นที่เป็นกลางสามารถแสดงได้เป็น (R + t) โดยใช้นิพจน์นี้ร่วมกับมุมการดัด ความยาวของส่วนโค้งชั้นที่เป็นกลาง (BA) สามารถแสดงได้เป็น:

• BA = Pi**(R+T)A/180

เพื่อให้การนิยามชั้นกลางของแผ่นโลหะมีความเรียบง่าย และถือว่าสามารถใช้ได้กับความหนาของวัสดุทุกชนิด จึงได้มีการนำแนวคิดเรื่องตัวประกอบ K เข้ามาใช้ คำนิยามเฉพาะคือ: ตัวประกอบ K คือ อัตราส่วนของความหนาของชั้นกลางของแผ่นโลหะต่อความหนาโดยรวมของวัสดุชิ้นส่วนแผ่นโลหะ กล่าวคือ:

• K = t/T

ดังนั้น ค่า K จะอยู่ระหว่าง 0 ถึง 1 เสมอ ตัวประกอบ K เท่ากับ 0.25 หมายความว่า ชั้นกลางตั้งอยู่ที่ 25% ของความหนาของวัสดุแผ่นโลหะของชิ้นงาน ในทำนองเดียวกัน หากค่าเท่ากับ 0.5 หมายความว่า ชั้นกลางตั้งอยู่ที่ 50% ของความหนาทั้งหมด เป็นต้น ด้วยการรวมสมการทั้งสองข้างต้น เราจะได้สมการต่อไปนี้ (8):

• BA = Pi(R+K*T)A/180 (8)

ค่าต่างๆ เหล่านี้ เช่น A, R และ T ถูกกำหนดโดยรูปร่างทางเรขาคณิตที่แท้จริง ดังนั้นกลับมาสู่คำถามเดิม อัตราส่วน K มาจากไหน? อีกครั้งคำตอบก็มาจากแหล่งข้อมูลเดิมๆ เช่น ผู้จัดจำหน่ายวัสดุโลหะแผ่น ข้อมูลการทดสอบ ประสบการณ์ คู่มือ และอื่นๆ อย่างไรก็ตาม ในบางกรณี ค่าที่ให้อาจไม่ใช่อัตราส่วน K โดยตรง หรืออาจไม่ได้แสดงในรูปแบบของสมการ (8) อย่างครบถ้วน แต่ถึงกระนั้น แม้ว่ารูปแบบการแสดงจะไม่เหมือนกันเป๊ะๆ เราก็สามารถหาความเชื่อมโยงระหว่างพวกมันได้เสมอ

ในการคำนวณการดัดแผ่นโลหะ เรามักต้องปรับค่า K factor แล้วทำไมเราจึงจำเป็นต้องปรับค่า K factor? เพราะการหักลดมุมโค้งที่ไม่ใช่มุม 90 องศาใน SW สามารถคำนวณได้โดยการป้อนค่าการหักลดหลายค่า ซึ่งยุ่งยากมาก เพื่อหลีกเลี่ยงค่าการหักลดมุมโค้งที่ไม่ใช่มุม 90 องศาของช่างเทคนิค เราจึงใช้ค่า K factor แทน ดังนั้นจะต้องนำทางค่า K factor อย่างแม่นยำสำหรับความหนาของแผ่นต่างๆ อย่างไร? สิ่งนี้จำเป็นต้องมีการปรับแต่ง การวิเคราะห์ต่อไปนี้แสดงให้เห็นถึงวิธีการปรับแต่ง:

1. ขั้นตอนแรกคือการกำหนดค่าจริงที่จำเป็นต้องหักสำหรับความหนาของแผ่นต่างๆ เช่น ค่าที่หักโดยการใช้มีด 6 เท่า สำหรับแผ่นเหล็กหนา 1.5 มม. คือ 2.5 มม.

2. ขั้นตอนที่สองคือการดีบัก K ใน SW เมื่อวาดชิ้นส่วนโลหะแผ่น ให้ตั้งค่ารัศมีด้านใน (inner R) เป็น 0.1 อย่างสม่ำเสมอเพื่อการดีบัก เนื่องจากค่า K จะแตกต่างกันไปตามรัศมีด้านในที่ต่างกัน คุณควรใส่ใจในจุดนี้ ดังนั้นให้ตั้งค่ารัศมีด้านในเป็น 0.1 อย่างสม่ำเสมอเพื่อการดีบัก จากนั้นบางคนอาจถามว่า หลังจากการดีบัก หากค่ารัศมีด้านในไม่ใช่ 0.1 จะทำให้ใช้ไม่ได้หรือไม่? ในกรณีนี้ ถ้าไม่ใช่ 0.1 คุณจำเป็นต้องเปลี่ยนเป็น 0.1 แล้วคลี่ชิ้นงานออก

3. ในขั้นตอนที่สามของการดีบัก ให้งอแผ่นขนาด 10x10 ที่มีความหนา 1.5 ใน SW โดยใช้รัศมี (R) เท่ากับ 0.1 มุม 90 องศา ค่าการหักลดการงอ (bending deduction) ถูกตั้งไว้ที่ 2.5 และผลลัพธ์ที่ได้จากการคลี่ชิ้นงานคือ 17.5 มม.

4. ขั้นตอนที่สี่คือการเปลี่ยนค่าการหักลดการงอ (bending deduction) เป็นปัจจัย K โดยเริ่มจากการตั้งค่าประมาณ เช่น 0.3 ซึ่งรูปร่างที่คลี่ออกจะไม่เท่ากับ 17.5 แน่นอน จากนั้นลองปรับค่า K อีกครั้งจนกว่าค่าที่ได้จะเท่ากับ 17.5 ด้วยวิธีนี้ ค่า K จะถูกปรับจนเป็น 0.23 ซึ่งเป็นค่าที่เหมาะสมที่ทำให้ชิ้นงานคลี่ออกมาได้พอดี 17.5 มม.

5. และดำเนินการในลักษณะเดียวกันนี้ต่อไป คุณสามารถดีบักตารางสถิติตัวเลขต่างๆ ได้