Štampač za savijanje

K faktor je nezavisna vrednost koja opisuje kako se savijanje lima savija/razvija pod širokim spektrom geometrijskih parametara. Takođe, to je nezavisna vrednost koja se koristi za izračunavanje kompenzacije savijanja (BA) u različitim uslovima, kao što su debljina materijala, poluprečnik savijanja/ugao savijanja itd. Slike 4 i 5 daju dublje razumevanje detaljne definicije K faktora.

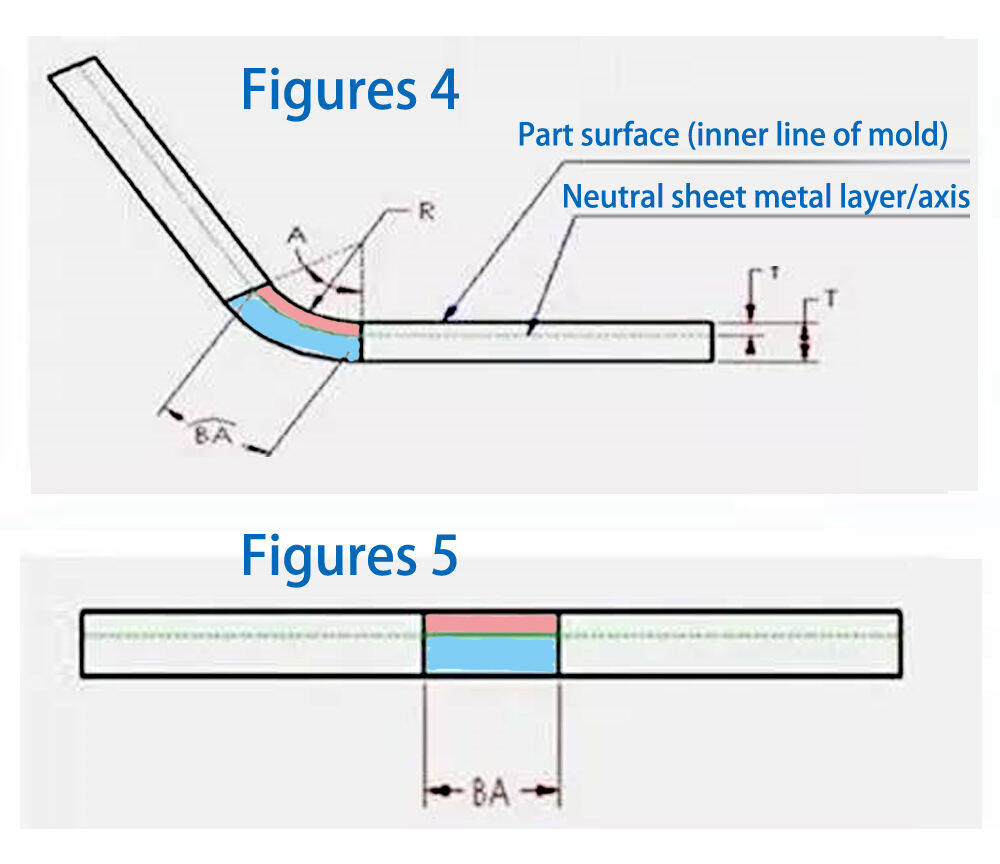
Унутар дебљине материјала лименог дела постоји нейтрални слој или оса. Овај нейтрални слој, који се налази у зони савијања, не издужује се ни не скраћује. То је једини део лима који се не деформише током савијања. На Сликама 4 и 5 ово је приказано као граница између розе и плаве области. Током процеса савијања, розе област се скраћује, док се плава област издужује. Ако се нейтрални слој не деформише, дужина лука у нейтралном слоју у зони савијања иста је у савијеном и развијеном стању. Стога, BA (компензација савијања) треба да буде једнака дужини лука у нейтралном слоју у зони савијања лименог дела. Овај лук је на Слици 4 приказан зеленом бојом. Положај нейтралног слоја зависи од специфичних особина материјала, као што је дуктилност. Претпоставимо да се нейтрални слој налази на растојању „t“ од површине, што значи да се дубина t мери од површине лименог дела ка унутрашњости дебљине лима. Стога се полупречник лука нейтралног слоја може изразити као (R + t). Коришћењем овог израза и угла савијања, дужина лука нейтралног слоја (BA) може се изразити као:

• BA = Pi**(R+T)A/180

Kako bi se pojednostavila definicija neutralnog sloja lima i smatrala primenljivom na sve debljine materijala, uveden je pojam K faktora. Konkretna definicija glasi: K faktor je odnos debljine neutralnog sloja lima i ukupne debljine materijala delova od lima, to jest:

• K = t/T

Stoga će vrednost K faktora uvek biti između 0 i 1. K faktor od 0,25 znači da se neutralni sloj nalazi na 25% debljine materijala lima dela. Slično tome, ako je 0,5, to znači da se neutralni sloj nalazi na 50% ukupne debljine, i tako dalje. Kombinovanjem ova dva izraza, možemo dobiti sledeću jednačinu (8):

• BA = Pi(R+K*T)A/180 (8)

Неколико ових вредности, као што су A, R и T, одређује се стварном геометријом. Дакле, враћајући се на првобитно питање, одакле потиче K фактор? И поново, одговор долази из истог старог извора: добављачи материјала за лимарске радове, тест подаци, искуство, упутства и тако даље. Међутим, у неким случајевима, дата вредност можда није очигледни K, нити је можда потпуно изражена у облику једначине (8). У сваком случају, чак и ако израз није потпуно исти, увек можемо пронаћи везу између њих.

У процесу прорачуна савијања лимова, често вршимо дебаговање К фактора. Зашто онда морамо да дебагујемо К фактор? Зато што се у СВ-у одузимање за савијање под углом који није 90 степени може израчунати само уносом више вредности одузимања, што је веома незгодно. Да би се избегла техничка вредност одузимања за савијање под углом који није 90 степени, користи се К фактор. Како онда тачно одредити К фактор за различите дебљине плоча? За то је потребно дебаговање. Доња анализа показује како извршити дебаговање:

1. Први корак је одређивање стварне вредности која треба да се одузме за различите дебљине плоча. На пример, вредност која се одузима код операције савијања шестоструког ножа за гвоздену плочу дебљине 1,5 мм износи 2,5 мм.

2. Други корак је да дебагујете K у SW. Када цртате лим, за потребе дебаговања униформно поставите унутрашњи R на 0,1. Зато што је K вредност различита за различите унутрашње R, треба обратити пажњу на ово. Тако да униформно поставите унутрашњи R на 0,1 за време дебаговања. Онда неки питaju, након дебаговања, ако унутрашњи R није 0,1, биће бескорисно? У том случају, ако није 0,1, морате га променити на 0,1 и развијти модел.

3. У трећем кораку дебаговања, у СW се савија плоча димензија 10*10 дебљине 1,5 са R од 0,1 под углом од 90 степени. Вредност опустања савијања постављена је на 2,5, а добијена развијена дужина је 17,5 мм.

4. Четврти корак је промена вредности опустања савијања на K фактор. Прво поставите приближну вредност, на пример 0,3. Развијени облик сигурно неће бити 17,5. Затим поново испробајте K вредност све док развијени облик не буде 17,5. На тај начин K вредност се подеси на 0,23, што је управо тачна вредност да би се добила развијена дужина од 17,5 мм.

5. И тако даље, можете дебаговати различите табеле нумеричких статистика.