Por que calibrar o fator K nos cálculos de dobra de chapa metálica?
O fator K é um valor independente que descreve como uma dobra em chapa metálica se curva/desdobra sob uma ampla gama de parâmetros geométricos. É também um valor independente utilizado para calcular a compensação de dobra (BA) sob uma ampla gama de condições, tais como espessura do material, raio de dobra/ângulo de dobra, etc. As Figuras 4 e 5 fornecem uma compreensão mais profunda da definição detalhada do fator K.
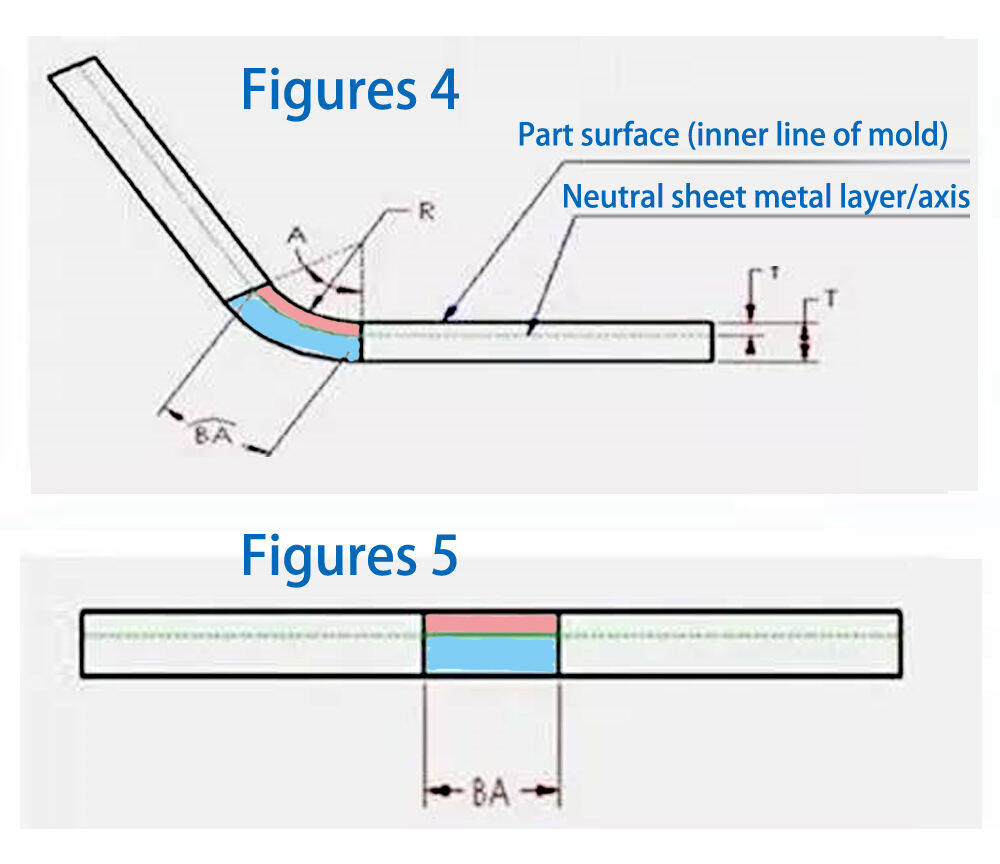
Dentro da espessura do material de uma peça de chapa metálica, existe uma camada ou eixo neutro. Esta camada neutra, localizada na zona de dobragem, não se alonga nem se comprime. Esta é a única área da chapa metálica que não sofre deformação durante a dobragem. Isso é representado nas Figuras 4 e 5 como o limite entre as áreas rosa e azul. Durante o processo de dobragem, a área rosa é comprimida, enquanto a área azul é esticada. Se a camada neutra não se deforma, o comprimento do arco na camada neutra na zona de dobragem é o mesmo nos estados dobrado e planificado. Portanto, BA (compensação de dobragem) deve ser igual ao comprimento do arco na camada neutra na zona de dobragem da peça de chapa metálica. Este arco é representado em verde na Figura 4. A localização da camada neutra depende das propriedades específicas do material, como ductilidade. Assuma que a camada neutra está localizada a uma distância "t" da superfície, ou seja, a profundidade t é medida a partir da superfície da peça de chapa metálica em direção à espessura da chapa. Portanto, o raio do arco da camada neutra pode ser expresso como (R + t). Usando esta expressão e o ângulo de dobragem, o comprimento do arco da camada neutra (BA) pode ser expresso como:
BA = Pi**(R+T)A/180
Para simplificar a definição da camada neutra da chapa metálica e considerá-la aplicável a todas as espessuras de material, introduz-se o conceito do fator K. A definição específica é: o fator K é a razão entre a espessura da camada neutra da chapa metálica e a espessura total do material da peça, ou seja:
K = t/T
Portanto, o valor de K estará sempre entre 0 e 1. Um fator K de 0,25 significa que a camada neutra está localizada a 25% da espessura do material da chapa metálica da peça. Da mesma forma, se for 0,5, significa que a camada neutra está localizada a 50% da espessura total, e assim por diante. Combinando as duas equações acima, podemos obter a seguinte equação (8):
BA = Pi(R+K*T)A/180 (8)
Vários desses valores, como A, R e T, são determinados pela geometria real. Então, voltando à pergunta original, de onde vem o fator K? Mais uma vez, a resposta vem das mesmas fontes antigas: fornecedores de materiais para chapas metálicas, dados de testes, experiência, manuais, entre outros. No entanto, em alguns casos, o valor fornecido pode não ser o óbvio K, nem estar totalmente expresso na forma da equação (8). Apesar disso, mesmo que a expressão não seja exatamente a mesma, sempre podemos encontrar uma conexão entre eles.
No processo de cálculo de dobragem de chapa metálica, frequentemente ajustamos o fator K. Por que precisamos ajustar o fator K? Porque a dedução de dobra não reta no SW só pode ser calculada mediante inserção de múltiplas deduções, o que é muito trabalhoso. Para evitar o uso do valor técnico de dedução em dobras não retas, utiliza-se em vez disso o fator K. Então, como orientar com precisão o fator K para diferentes espessuras de chapa? Isso exige ajuste. A análise a seguir mostra como fazer esse ajuste:
1. O primeiro passo é determinar o valor real que precisa ser subtraído para diferentes espessuras de chapa. Por exemplo, o valor subtraído pela operação com faca de 6 vezes para uma chapa de ferro de 1,5 mm de espessura é 2,5 mm.
2. O segundo passo é depurar o K no SW. Ao desenhar chapa metálica, defina uniformemente o raio interno como 0,1 para depuração. Como o valor de K varia conforme o raio interno, você deve prestar atenção a isso. Portanto, defina uniformemente o raio interno como 0,1 para depuração. Algumas pessoas perguntam então: após a depuração, se o raio interno não for 0,1, será inútil? Nesse caso, se não for 0,1, você precisa alterá-lo para 0,1 e desdobrá-lo.
3. Na terceira etapa de depuração, uma placa de 10*10 com espessura de 1,5 é dobrada no SW com um raio de 0,1 em um ângulo de 90 graus. A dedução de dobra é definida como 2,5, e o resultado do desdobramento é 17,5 mm.
4. O quarto passo é alterar a dedução de dobra para fator K. Primeiro defina um valor aproximado, por exemplo, 0,3. A forma desdobrada certamente não será 17,5. Em seguida, teste novamente o valor de K até que o resultado seja 17,5. Dessa forma, o valor de K é ajustado para 0,23, que é exatamente o necessário para obter 17,5 mm no desdobramento.
5. E assim sucessivamente, você pode depurar diferentes tabelas estatísticas de valores numéricos.


















































