מכבש לחץ

גורם K הוא ערך עצמאי המתאר כיצד כיפוף של לוח מתכת מכופף/מתפזר תחת טווח רחב של פרמטרים גאומטריים. זהו גם ערך עצמאי המשמש לחישוב פיצול כיפוף (BA) תחת מגוון תנאים, כגון עובי חומר, רדיוס כיפוף/זווית כיפוף, וכו'. איורים 4 ו-5 מספקים הבנה מעמיקה יותר של ההגדרה המפורטת של גורם K.

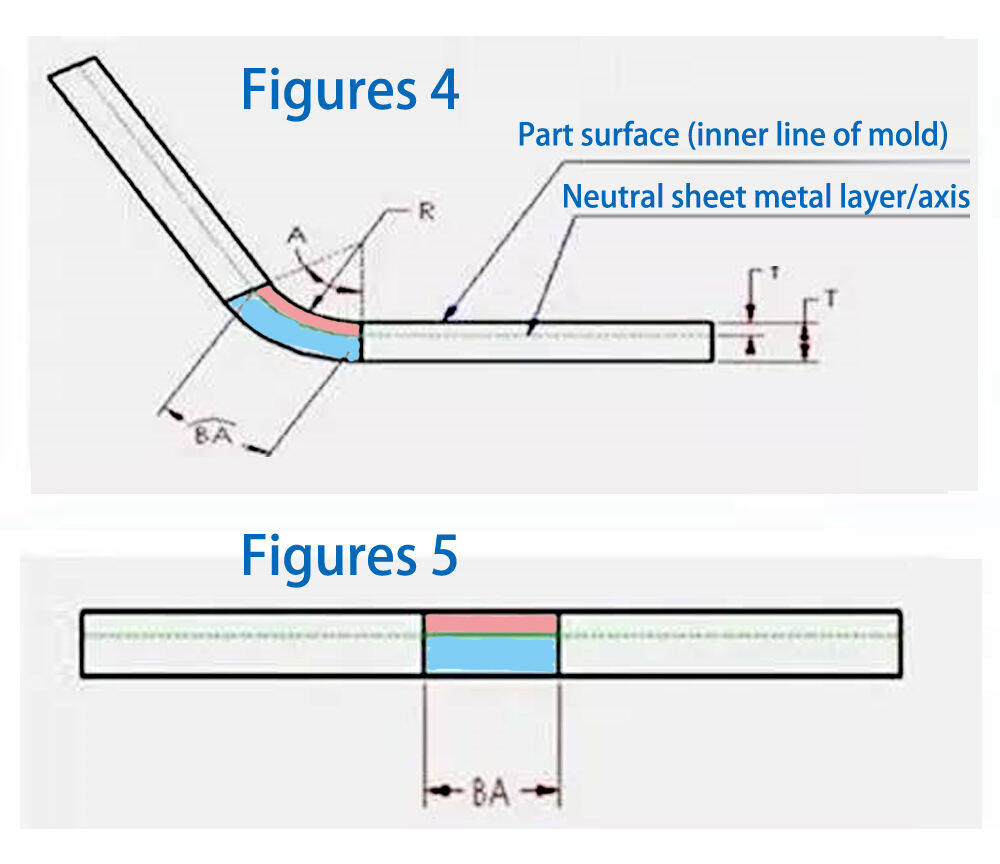
בתוך עובי החומר של חלק מתכת דק, קיים שכבת ניטרלית או ציר ניטרלי. השכבה הניטרלית הזו, שנמצאת באזור הקיפול, לא נמתחת ולא מתכווצת. זהו האזור היחיד במתכת הדק שאינו מתעוות במהלך הקיפול. זה מוצג באיורים 4 ו-5 כקו הגבול בין האזורים הוורוד והכחול. במהלך תהליך הקיפול, האזור הוורוד מתקצר, בעוד שהאזור הכחול נמתח. אם השכבה הניטרלית אינה מתעortion, אורך הקשת בשכבה הניטרלית באזור הקיפול הוא אותו אורך גם במצב מקופל וגם במצב שטוח. לכן, BA (היתר קיפול) צריך להיות שווה לאורך הקשת בשכבה הניטרלית באזור הקיפול של חלק מתכת הדק. קשת זו מוצגת בצבע ירוק באיור 4. מיקום השכבה הניטרלית תלוי בתכונות חומר ספציפיות, כגון דUCTILITY. נניח שהשכבה הניטרלית נמצאת במרחק "t" מפני השטח, כלומר העומק t נמדד מפני השטח של חלק מתכת הדק פנימה לעבר עובי המתכת. לכן, רדיוס קשת השכבה הניטרלית ניתן להבעה כ-(R + t). בעזרת ביטוי זה וזוית הקיפול, ניתן להביע את אורך קשת השכבה הניטרלית (BA) כ:

• BA = Pi**(R+T)A/180

כדי לפשט את ההגדרה של השכבה הנייטרלית של דף מתכת ולשקול אותה תקפה לכל עובי חומר, מוצג מושג מקדם K. ההגדרה הספציפית היא: מקדם K הוא היחס בין עובי השכבה הנייטרלית של דף המתכת לעובי הכולל של חומר החלק של דף המתכת, כלומר:

• K = t/T

לכן, ערך ה-K תמיד יהיה בין 0 ל-1. מקדם K של 0.25 אומר שהשכבה הנייטרלית נמצאת ב-25% מעובי חומר דף המתכת של החלק. באופן דומה, אם הערך הוא 0.5, זה אומר שהשכבה הנייטרלית נמצאת ב-50% מעובי הכוללת, וכן הלאה. על ידי שילוב שני המשוואות שלעיל, ניתן לקבל את המשוואה הבאה (8):

• BA = Pi(R+K*T)A/180 (8)

כמה מהערכים האלה, כגון A, R ו-T, נקבעים על פי הגאומטריה בפועל. אם כן, חזרה לשאלה המקורית, מאיפה מגיע מקדם K? שוב, התשובה מגיעה מאותם מקורות ישנים: ספקים של חומר לפלטות מתכת, נתוני בדיקה, ניסיון, חוברות טכניות וכן הלאה. עם זאת, במקרים מסוימים ערך נתון עשוי שלא להיות K המוכר, או שלא יופיע בצורה מפורשת של משוואה (8). בכל אופן, גם אם הביטוי אינו זהה בדיוק, תמיד נוכל למצוא קשר ביניהם.

בתהליך חישוב כיפוף של דוכן מתכת, אנו לעיתים קרובות מבצעים דיבאג לפקטור K. אז למה אנו צריכים לבצע דיבאג לפקטור K? מכיוון שחיסור כיפוף שאינו בזווית 90 מעלות ב-SW ניתן לחישוב רק על ידי הזנת מספר חיסורים, מה שמאוד מסורבל. על מנת להימנע מערכי חיסור טכניים של כיפוף שאינם בזווית 90 מעלות, משתמשים בפקטור K במקום זאת. אז כיצד ניתן להדריך באופן מדויק את פקטור K עבור עובי לוחות שונים? לשם כך נדרש דיבאג. הניתוח הבא מראה כיצד לבצע דיבאג:

1. הצעד הראשון הוא לקבוע את הערך האמיתי שיש לחסר עבור עובי לוחות שונים. למשל, הערך הנחסר בפעולת סכין 6-כפולה עבור לוח ברזל בעובי 1.5 מ"מ הוא 2.5 מ"מ.

2. הצעד השני הוא איתור שגיאות ב-K בתוכנת SW. בעת ציור גיליונות מתכת, יש לקבוע באופן אחיד את רדיוס הפנימי (R) ל-0.1 לצורך איתור שגיאות. מאחר והערך K משתנה בהתאם לרדיוס הפנימי, יש להקפיד על נקודה זו. לכן, יש לקבוע באופן אחיד את רדיוס הפנימי (R) ל-0.1 לצורך איתור שגיאות. אז אנשים שואלים: לאחר הסיום של איתור השגיאות, אם רדיוס הפנימי אינו 0.1, האם זה יפסול את התוצאה? במקרה כזה, אם הרדיוס אינו 0.1, יש לשנות אותו ל-0.1 ולפתוח את הגיליון.

3. בשלב השלישי של איתור שגיאות, מבצעים כיפוף של לוח בגודל 10*10 ובעובי 1.5 בתוכנת SW, עם רדיוס כיפוף (R) של 0.1 בזווית 90 מעלות. ירידת הכיפוף מוגדרת ל-2.5, והתוצאה של הפעלה היא 17.5 מ"מ.

4. הצעד הרביעי הוא שינוי ערך ירידת הכיפוף לגורם K. ראשית, מגדירים ערך משוער, למשל 0.3. ברור שהגודל המופעל לא יהיה 17.5. לאחר מכן מנסים שוב ערכים שונים של K עד שמגיעים ל-17.5. בדרך זו, ערך ה-K מותאם ל-0.23, מה שנותן בדיוק את הפעלה של 17.5 מ"מ.

5. וכן הלאה, ניתן לבצע איתור שגיאות בטבלאות מספריות שונות.