Survekaar

K-tegur on sõltumatu väärtus, mis kirjeldab, kuidas lehtmetalli paind paindub/laieneb laia spektri geomeetriliste parameetrite mõjul. See on samuti sõltumatu väärtus, mida kasutatakse painde kompenseerimise (BA) arvutamiseks laia spektri tingimustel, nagu materjali paksus, painde raadius/painde nurk jne. Joonised 4 ja 5 annavad sügavamat ülevaadet K-teguri üksikasjalikust definitsioonist.

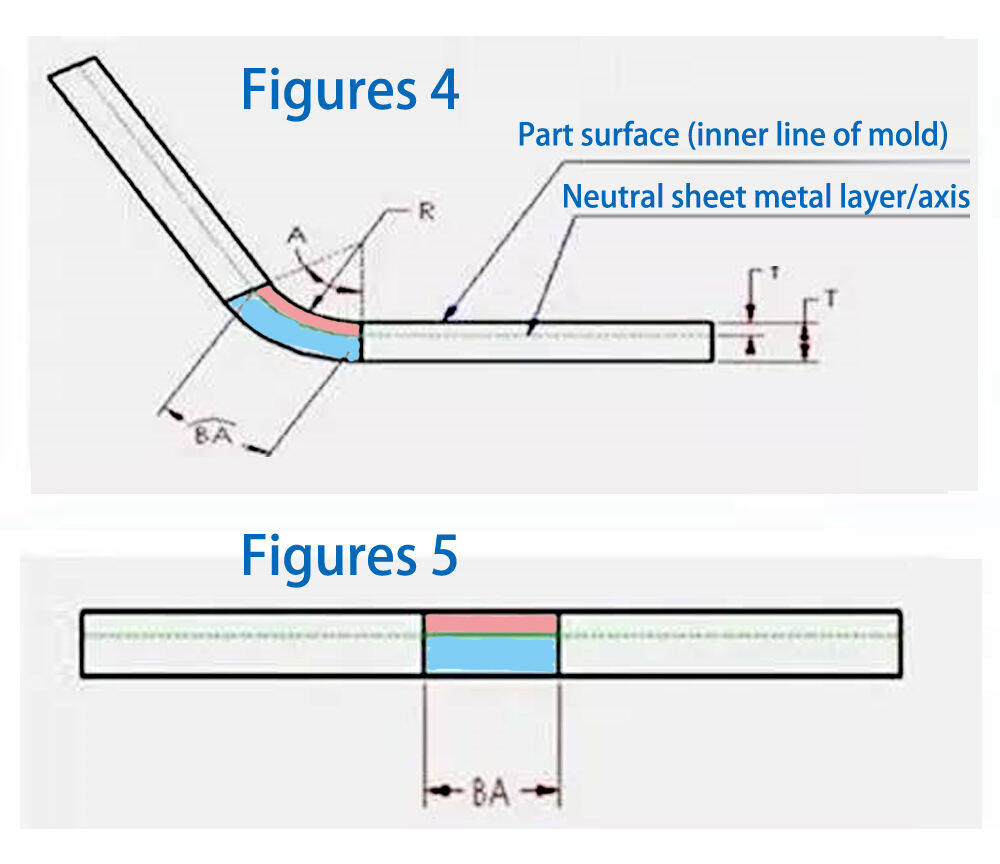
Plekkdetali materjali paksuses asub neutraalne kiht või telg. See neutraalne kiht, mis asub paindutsoonis, ei veni ega tõmbu kokku. See on ainsamas kohas, kus plekist detail ei deformatsioonu paindutamisel. Seda kujutatakse joonistel 4 ja 5 piirjoonena roosaka ja sinise ala vahel. Paine protsessi jooksul tõmbub roosakas ala kokku, samas kui sinine ala venib. Kui neutraalkiht ei deformatsioonu, siis painetsoonis oleva neutraalkihiga kaar on nii painutatud kui ka sirgjoondunud olekus sama pikk. Seetõttu peaks BA (painekompenatsioon) võrduma plekkdetali painetsoonis oleva neutraalkihiga kaare pikkusega. See kaar on esitatud rohelisena joonisel 4. Neutraalkihiga asukoht sõltub konkreetsete materjalide omadustest, näiteks plastilisusest. Eeldame, et neutraalkiht asub kaugusel "t" pinnast, mis tähendab, et sügavus t mõõdetakse plekkdetali pinnast materjali paksusesse. Seega saab neutraalkihiga kaare raadiuse avaldada kui (R + t). Kasutades seda avaldist ja paine nurka, saab neutraalkihiga kaare pikkuse (BA) avaldada järgmiselt:

• BA = Pi**(R+T)A/180

Pliidi neutraalkihi määratluse lihtsustamiseks ja selle kohaldamiseks kõikidele materjalipaksustele kasutatakse K-teguri mõistet. Täpne definitsioon on järgmine: K-tegur on pliiatsi neutraalkihi paksuse suhe teraseosa materjali üldpaksusele, see tähendab:

• K = t/T

Seega jääb K väärtus alati vahemikku 0 kuni 1. K-tegur 0,25 tähendab, et neutraalkihk asub detaili pliiatsmaterjali paksuse 25% juures. Samamoodi tähendab väärtus 0,5, et neutraalkihk asub 50% juures kogupaksusest jne. Ühendades need kaks võrrandit, saame järgmise võrrandi (8):

• BA = Pi(R+K*T)A/180 (8)

Mõned neist väärtustest, nagu A, R ja T, määratakse tegeliku geomeetriaga. Tagasi algküsimuse juurde: kust tuleb K-tegur? Jällegi tuleb vastus samadest vanadest allikatest: lehtmetallide tarnijatest, testimisandmetest, kogemusest, juhenditest jne. Siiski võib mõnel juhul antud väärtus olla mitte ilmne K ega väljendatud täielikult võrrandina (8). Igatahes, isegi kui avaldis pole täpselt sama, saame alati nende vahel leida seose.

Lehtmetalli painamise arvutamise protsessis silume sageli K-tegurit. Miks meil on vaja K-tegurit seadistada? Kuna SW-s saab mitte-90-kraadise painde mõõdu arvutada ainult mitme lahutusmõõduna, mis on väga tülikas. Tehnilise mitte-90-kraadise paindemõõdu vältimiseks kasutatakse selle asemel K-tegurit. Kuidas siis täpselt juhendada K-tegurit erinevatele plaatide paksustele? Selleks on vaja silumist. Järgnev analüüs näitab, kuidas seda teha:

1. Esimene samm on kindlaks teha tegelik väärtus, mida tuleb erinevate plaatide paksuste puhul lahutada. Näiteks 1,5 mm paksu raudplaat üheksakordse noaga töötlemisel lahutatav väärtus on 2,5 mm.

2. Teine samm on K silumine tarkvaras. Pliidilehe joonistamisel seadke silumise ajaks sisemine R ühtlaselt 0,1. Kuna erinevate sisemiste R väärtuste korral on K väärtus erinev, tuleb sellele tähelepanu pöörata. Seega seadke silumiseks sisemine R ühtlaselt 0,1. Siis küsivad mõned inimesed, kas see on asjatu, kui sisemine R pole 0,1? Sel juhul, kui see ei ole 0,1, peate selle muutma 0,1-ks ja laiendama.

3. Kolmandas silumissammus painutatakse 10*10 plaat, mille paksus on 1,5, tarkvaras nurga all 90 kraadi R=0,1-ga. Paindumisarvestuseks seatud väärtus on 2,5 ning saadud laiendatud mõõt on 17,5 mm.

4. Neljas samm on paindumisarvestuse muutmine K-teguriks. Esiteks seatud ligikaudne väärtus, näiteks 0,3. Laiendatud kuju pole kindlasti 17,5. Seejärel proovige uuesti K väärtust, kuni see on 17,5. Nii justkui K väärtus on reguleeritud 0,23-le, on see täpselt sobiv, et laiendatud mõõt oleks 17,5 mm.

5. Ja nii edasi, võite siluda erinevaid numbrilisi statistikatabelid.