Γιατί να βαθμονομήσετε τον παράγοντα K στους υπολογισμούς κάμψης ελασμάτων;
Ο συντελεστής K είναι μια ανεξάρτητη τιμή που περιγράφει πώς ένα ελάσματος λυγίζει/ξετυλίγεται υπό ένα ευρύ φάσμα γεωμετρικών παραμέτρων. Είναι επίσης μια ανεξάρτητη τιμή που χρησιμοποιείται για τον υπολογισμό της αντιστάθμισης λυγίσματος (BA) υπό μια ποικιλία συνθηκών, όπως πάχος υλικού, ακτίνα λυγίσματος/γωνία λυγίσματος, κ.λπ. Τα σχήματα 4 και 5 παρέχουν μια βαθύτερη κατανόηση του λεπτομερούς ορισμού του συντελεστή K.
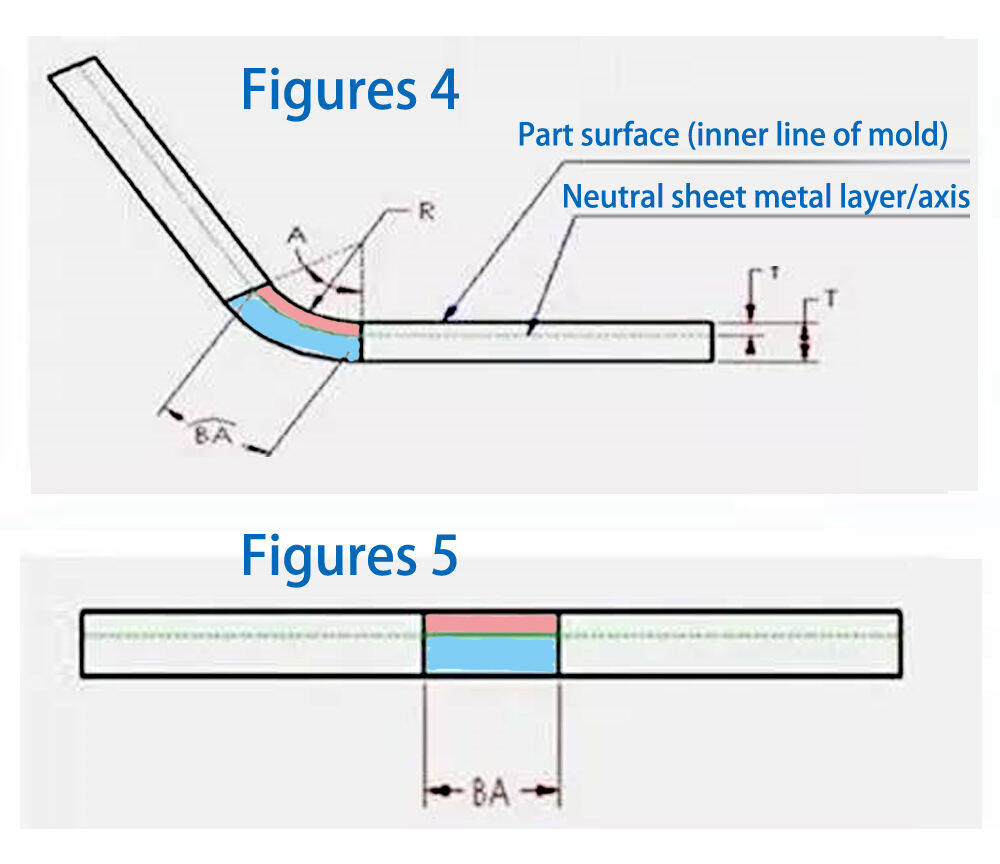
Μέσα στο πάχος του υλικού ενός ελάσματος, υπάρχει ένα ουδέτερο στρώμα ή άξονας. Αυτό το ουδέτερο στρώμα, που βρίσκεται στη ζώνη κάμψης, δεν επιμηκύνεται ούτε συμπιέζεται. Πρόκειται για τη μόνη περιοχή του ελάσματος που δεν παραμορφώνεται κατά τη διαδικασία κάμψης. Αυτό απεικονίζεται στα Σχήματα 4 και 5 ως το όριο μεταξύ των ροζ και μπλε περιοχών. Κατά τη διαδικασία κάμψης, η ροζ περιοχή συμπιέζεται, ενώ η μπλε περιοχή επιμηκύνεται. Εάν το ουδέτερο στρώμα δεν παραμορφώνεται, το μήκος του τόξου στο ουδέτερο στρώμα στη ζώνη κάμψης είναι το ίδιο τόσο στη λυγισμένη όσο και στην ανεπτυγμένη κατάσταση. Ως εκ τούτου, το BA (αντιστάθμιση κάμψης) πρέπει να είναι ίσο με το μήκος του τόξου στο ουδέτερο στρώμα στη ζώνη κάμψης του εξαρτήματος ελάσματος. Αυτό το τόξο απεικονίζεται με πράσινο χρώμα στο Σχήμα 4. Η θέση του ουδέτερου στρώματος εξαρτάται από συγκεκριμένες ιδιότητες του υλικού, όπως η πλαστικότητα. Υποθέτουμε ότι το ουδέτερο στρώμα βρίσκεται σε απόσταση «t» από την επιφάνεια, πράγμα που σημαίνει ότι το βάθος t μετριέται από την επιφάνεια του εξαρτήματος ελάσματος προς το εσωτερικό του πάχους του ελάσματος. Ως εκ τούτου, η ακτίνα του τόξου του ουδέτερου στρώματος μπορεί να εκφραστεί ως (R + t). Χρησιμοποιώντας αυτή την έκφραση και τη γωνία κάμψης, το μήκος του τόξου του ουδέτερου στρώματος (BA) μπορεί να εκφραστεί ως:
BA = Pi**(R+T)A/180
Για να απλοποιηθεί ο ορισμός του ουδέτερου επιπέδου του ελάσματος και να θεωρηθεί εφαρμόσιμος σε όλα τα πάχη υλικού, εισάγεται η έννοια του συντελεστή K. Ο συγκεκριμένος ορισμός είναι: ο συντελεστής K είναι ο λόγος του πάχους του ουδέτερου επιπέδου του ελάσματος προς το συνολικό πάχος του υλικού του εξαρτήματος από ελάσμα, δηλαδή:
K = t/T
Επομένως, η τιμή του K θα βρίσκεται πάντα μεταξύ 0 και 1. Ένας συντελεστής K 0,25 σημαίνει ότι το ουδέτερο επίπεδο βρίσκεται στο 25% του πάχους του υλικού ελάσματος του εξαρτήματος. Παρόμοια, αν είναι 0,5, σημαίνει ότι το ουδέτερο επίπεδο βρίσκεται στο 50% του συνολικού πάχους, και ούτω καθεξής. Συνδυάζοντας τις δύο παραπάνω εξισώσεις, μπορούμε να πάρουμε την ακόλουθη εξίσωση (8):
BA = Pi(R+K*T)A/180 (8)
Πολλές από αυτές τις τιμές, όπως οι A, R και T, καθορίζονται από την πραγματική γεωμετρία. Επομένως, επιστρέφοντας στην αρχική ερώτηση, από πού προέρχεται ο συντελεστής K; Και πάλι, η απάντηση προέρχεται από τις ίδιες παλιές πηγές: προμηθευτές υλικών λαμαρίνας, δοκιμαστικά δεδομένα, εμπειρία, εγχειρίδια και ούτω καθεξής. Ωστόσο, σε ορισμένες περιπτώσεις, η δεδομένη τιμή ενδέχεται να μην είναι ο προφανής K, ούτε ενδέχεται να εκφράζεται πλήρως με τη μορφή της εξίσωσης (8). Παρ' όλα αυτά, ακόμη κι αν η έκφραση δεν είναι ακριβώς η ίδια, μπορούμε πάντα να βρούμε μια σύνδεση μεταξύ τους.
Κατά τη διαδικασία υπολογισμού λυγίσματος ελασμάτων, συχνά ρυθμίζουμε τον παράγοντα Κ. Γιατί λοιπόν χρειάζεται να ρυθμίσουμε τον παράγοντα Κ; Επειδή η αφαίρεση καμπτόμενης μή-90 μοιρών στο SW μπορεί να υπολογιστεί μόνο με την εισαγωγή πολλαπλών αφαιρέσεων, κάτι το οποίο είναι πολύ επίπονο. Για να αποφευχθεί η τεχνική τιμή αφαίρεσης καμπτόμενης μή-90 μοιρών, χρησιμοποιείται αντ' αυτού ο παράγοντας Κ. Πώς λοιπόν μπορούμε να καθοδηγήσουμε με ακρίβεια τον παράγοντα Κ για διαφορετικά πάχη πλακών; Αυτό απαιτεί ρύθμιση. Η παρακάτω ανάλυση δείχνει πώς να γίνει η ρύθμιση:
1. Το πρώτο βήμα είναι να καθοριστεί η πραγματική τιμή που πρέπει να αφαιρεθεί για διαφορετικά πάχη πλακών. Για παράδειγμα, η τιμή που αφαιρείται από τη λειτουργία 6-πλής λεπίδας για ελάσματος σιδήρου πάχους 1,5 mm είναι 2,5 mm.
2. Το δεύτερο βήμα είναι να εντοπίσετε σφάλματα στο K στο SW. Όταν σχεδιάζετε λαμαρίνα, ορίστε ομοιόμορφα την εσωτερική ακτίνα R σε 0,1 για τη διαδικασία εντοπισμού σφαλμάτων. Επειδή η τιμή K διαφέρει για διαφορετικές τιμές εσωτερικής ακτίνας R, πρέπει να το λάβετε υπόψη. Οπότε ορίστε ομοιόμορφα την εσωτερική ακτίνα R σε 0,1 για τη διαδικασία εντοπισμού σφαλμάτων. Μετά κάποιοι ρωτούν, μετά τον εντοπισμό σφαλμάτων, αν η εσωτερική ακτίνα R δεν είναι 0,1, θα είναι άχρηστο; Σε αυτήν την περίπτωση, αν δεν είναι 0,1, πρέπει να την αλλάξετε σε 0,1 και να κάνετε την ανάπτυξη.
3. Στο τρίτο βήμα εντοπισμού σφαλμάτων, ένα πλάκα 10*10 πάχους 1,5 λυγίζεται στο SW με ακτίνα R 0,1 σε γωνία 90 μοιρών. Η αφαίρεση λυγίσματος ορίζεται σε 2,5, και το αποτέλεσμα της ανάπτυξης είναι 17,5 mm.
4. Το τέταρτο βήμα είναι να αλλάξετε την αφαίρεση λυγίσματος σε συντελεστή K. Πρώτα ορίστε μια προσεγγιστική τιμή, για παράδειγμα, 0,3. Το ανεπτυγμένο σχήμα σίγουρα δεν θα είναι 17,5. Στη συνέχεια δοκιμάστε ξανά την τιμή K μέχρι να γίνει 17,5. Με αυτόν τον τρόπο, η τιμή K ρυθμίζεται σε 0,23, η οποία είναι ακριβώς η σωστή τιμή για να αναπτυχθεί σε 17,5 mm.
5. Και ούτω καθεξής, μπορείτε να εντοπίσετε σφάλματα σε διαφορετικούς πίνακες αριθμητικών δεδομένων.


















































